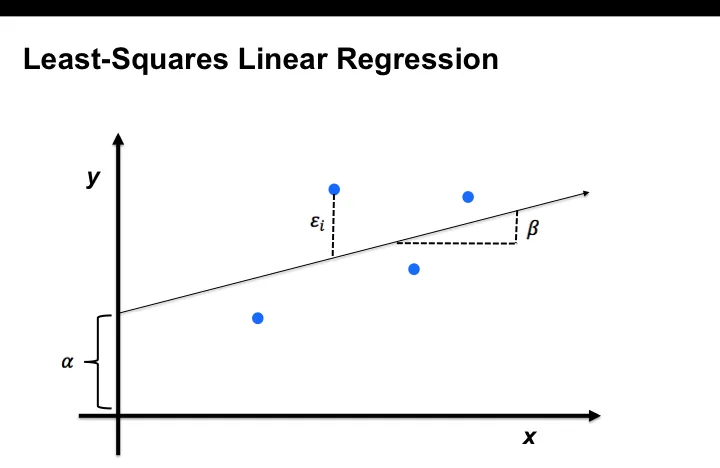
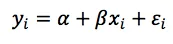Least-Squares Functions

The least-squares method of linear regression attempts to fit a linear regression trend line as closely as possible. This line has the smallest possible value for the sum of the squares of the errors between the predicted value of the line and the actual two-dimensional data points.

In the following diagram, the least-squares linear regression plots a line through the set of points that minimizes the sum of the squares of the error factors.

Diagram showing a least-squares linear regression line running through a set of plotted points. The line minimizes the sum of the squared vertical distances between the points and the line.

The actual data points are calculated using the following equation:

Equation for a simple linear regression model showing yi equals alpha plus beta times xi plus epsilon i, where yi is the dependent variable, xi is the independent variable, alpha is the intercept, beta is the slope, and epsilon i is the error term.

Use the R-squared function (RSQ) that returns square of the correlation coefficient to measure how well the linear regression expresses the variability of the Y values around their mean.

  • RSQ (*numeric1*, *numeric2*)

    • where numeric1 and numeric2 are facts or metrics

    • Computes the R-squared value for the two sets of numeric values. Also known as the coefficient of determination, R-squared ranges between 0 and 1, with a value of 1 indicating that the model explains all variability in the dependent variables data.

      R-squared does not determine if there is bias in the estimates.

Syntax 

SELECT RSQ(metric1, metric2)
SELECT RSQ(fact1, metric2)
SELECT RSQ(fact1, fact2)

Examples 

SELECT RSQ({metric/count_of_defects}, {metric/production_volume})
Covariance Functions
Standard Deviation Functions